Options Greeks - Gamma

Here is the next part of the options trading playbook. We have discussed the meaning of option greeks and the first option greeks in our earlier blog. Continuing with the series, we will discuss the next level of option greeks, the ‘Gamma Greek’. Read on to learn more about this term and its importance in options trading.

Read More: Doji Candlesticks - All you need to know

What is Gamma Greek?

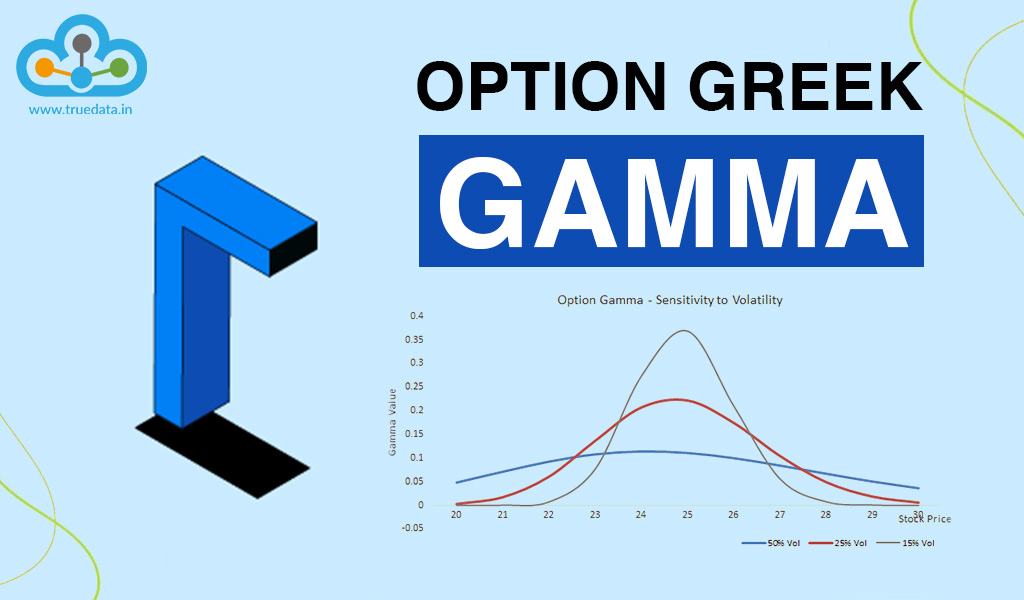
Delta in option greeks measures the change in the options price to the change in the underlying asset. Gamma greek, on the other hand, is the measure of how quickly an option's delta can change in response to changes in the underlying asset's price. If the gamma is high, it means the option's value can change rapidly with even small price movements. On the other hand, if the gamma is low, the option's value will not change much, even if the price of the underlying asset moves. It's important to understand gamma because it affects the risk and potential profits of an options position. Higher gamma means the option's value can swing more dramatically, which can be both good and bad. It offers the potential for larger profits if the price moves in favor of the trader, but it also means the option's value can decrease quickly if the price movement is adverse.

How to calculate Gamma Greek?

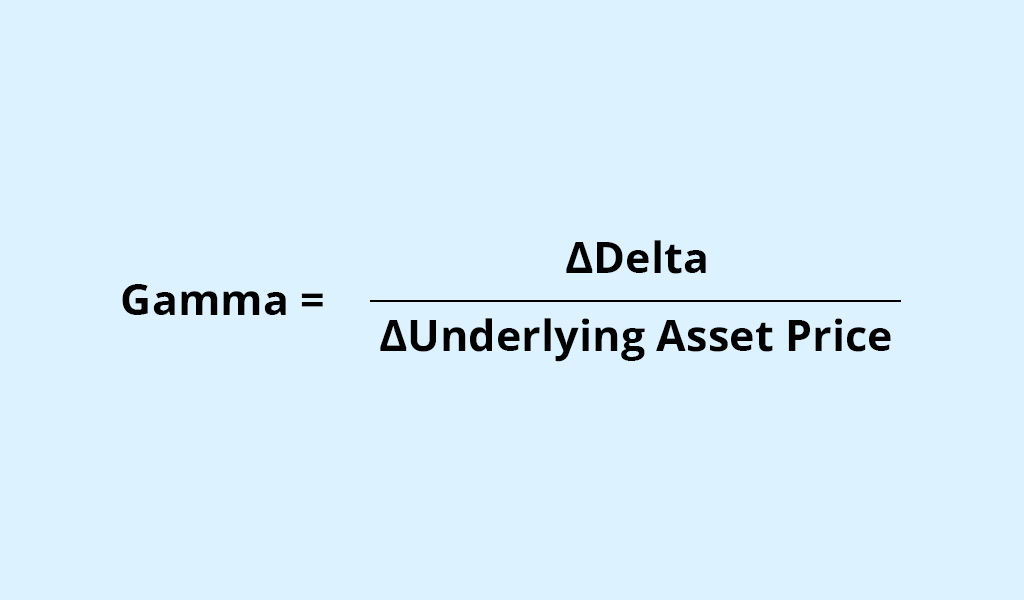
Gamma = (?Delta) / (?Underlying Asset Price)

Here's an example to illustrate the calculation of Gamma for an option:

Let's assume a trader has purchased a call option on a stock. The option has the following details - 

Option Price (V) - Rs. 10.00

Underlying Stock Price (S) -  Rs. 100.00

Delta (Δ): 0.5

Now, let's consider two scenarios where the stock price changes:

Scenario 1 - The stock price increases by Rs. 1.00 to Rs. 101.00.

Scenario 2 - The stock price increases further by Rs. 1.00 to Rs. 102.00.

To calculate Gamma, you need to determine the change in Delta (Δ) for a given change in the underlying stock price (?Underlying Asset Price).

Calculate the Delta value for the first scenario:

Delta 1 = ?V1 / ?S1 = (New Option Price - Option Price) / (New Stock Price - Stock Price)

Delta 1 = (?V1) / (?S1) = (Rs. 10.50 - Rs. 10.00) / (Rs. 101.00 - Rs. 100.00)

Delta 1 = Rs. 0.50 / Rs. 1.00 = 0.50

Calculate the Delta value for the second scenario:

Delta 2 = ?V2 / ?S2 = (New Option Price - Option Price) / (New Stock Price - Stock Price)

Delta 2 = (?V2) / (?S2) = (Rs. 11.00 - Rs. 10.50) / (Rs. 102.00 - Rs. 101.00) 

Delta 2 = Rs. 0.50 / Rs. 1.00 = 0.50

Now, calculate the change in Delta (?Delta) by subtracting Delta 2 from Delta 1:

?Delta = Delta 1 - Delta 2 = 0.50 - 0.50 = 0.00

Finally, calculate Gamma using the formula mentioned earlier:

Gamma = (?Delta) / (?Underlying Asset Price) 

Gamma = 0.00 / Rs. 1.00 = 0.00

In this example, the calculated Gamma is zero. This implies that Delta does not change significantly with small movements in the stock price. It indicates that the option's value is not very sensitive to changes in the underlying asset's price.

Interpretation of Gamma Greek

Interpreting Gamma Greeks in options trading involves understanding how the Gamma of an option can impact its Delta and the relationship between price changes of the underlying asset and the option's value. Gamma represents the rate at which an option's Delta changes in response to price movements in the underlying asset. The interpretation of gamma greeks is explained here. 

High and low Gamma values

High Gamma values indicate that an option's Delta can change rapidly, leading to larger potential gains or losses. Low Gamma values suggest that an option's Delta is more stable and less affected by small price movements.

Gamma and price movements

Gamma is highest for at-the-money options, where the strike price is close to the current underlying asset's price. It decreases for options that are deep in or out-of-the-money. This means that at-the-money options are more sensitive to price movements, while deep in or out-of-the-money options have lower sensitivity.

Impact of Gamma

Gamma has a significant impact on the stability of an option's value. Options with higher Gamma are more volatile and prone to larger price swings, while options with lower Gamma are more stable and less affected by small price fluctuations.

Gamma and time decay

Gamma can also affect the time decay or Theta of options. As expiration approaches, options with high Gamma may experience more rapid changes in Delta and, consequently, their time value can erode quickly. This effect is important to consider when evaluating the impact of time decay on option prices.

What are the uses of gamma greeks in option trading?

Using Gamma Greeks in option trading can help traders assess and manage their risks and potential rewards associated with their options positions. Here's how to utilize Gamma in option trading.

Risk-reward assessment 

Gamma helps traders evaluate the potential risks and rewards associated with their options positions. Higher Gamma values imply higher sensitivity to price changes, which can lead to larger profits or losses. By considering Gamma, traders can assess the level of risk they are exposed to and determine the potential profitability of their trades.

Adjusting position size

Gamma assists in determining the appropriate position size based on risk tolerance. Options with higher Gamma exhibit greater fluctuations in their price sensitivity to the underlying asset, requiring smaller position sizes to manage risk. Options with lower Gamma offer more stability and can accommodate larger positions.

Managing delta

Gamma is instrumental in managing Delta, which measures the change in an option's price for a given change in the underlying asset's price. By understanding Gamma, traders can anticipate how Delta will change with different price movements. This knowledge enables them to adjust their positions and maintain the desired risk exposure.

Hedging strategies

Gamma plays a vital role in delta hedging strategies. Traders use Gamma to determine the necessary adjustments in their positions of the underlying asset to maintain a delta-neutral position. This helps protect against adverse price movements and effectively manage risk.

Understanding the entry and exit points of a trade

Gamma provides insights into timing option trades. Options with higher Gamma tend to exhibit more significant price swings, making them attractive for short-term trading strategies or capitalizing on market volatility. Traders can utilize Gamma to determine suitable entry and exit points for their trades.

Managing time decay

As options approach expiration, Gamma tends to increase. This implies that the sensitivity of an option's price to changes in the underlying asset's price becomes more pronounced. Traders must consider Gamma when managing the impact of time decay on their options positions, as it affects the potential erosion of time value.

Portfolio risk management

Gamma Greeks assist traders in evaluating and managing the overall risk exposure of their options portfolio. By analyzing the Gamma values of individual options and their combined impact, traders can make informed decisions to balance and diversify their portfolios effectively, thereby mitigating risks.

Conclusion

Gamma greeks are the next stage or level of greeks which helps in understanding option trading and effectively implementing strategies to create a successful portfolio. Moving forward we will also discuss the further levels of option greeks and their impact on option trading for traders and the market as a whole.  We hope this blog was able to provide you with a basic understanding of gamma greeks and their use in option trading. Let us know if you need any further information or have any queries relating to the same.  Till then Happy Reading!